hwaswitch.blogg.se - Efficient rsa decryption python 3

"""Generate a prime candidate not divisible by first primes""" It aborts back to the outer loop immediately upon failure, from there it calls the function in the first step to generate the next candidate odd number and test again. The inner for loop runs the test with the elements of the prime array one by one. It defines an array with elements of 50 prime numbers after 2, then uses a double loop in the function to implement the basic primality test. '''Generate a random odd number in the range ''' It also sets the step size to 2 to ensure that only n-bit random odd values are returned. The function uses the input number of bits n in the exponents of 2, which specify the start and end values of randrange(). The whole process is shown in the following flowchart.įor the first step, Python function programming requires importing the library function randrange() from the random library. Also for demonstration purposes, the second step uses the first 50 prime numbers greater than 2 for the basic primality test.

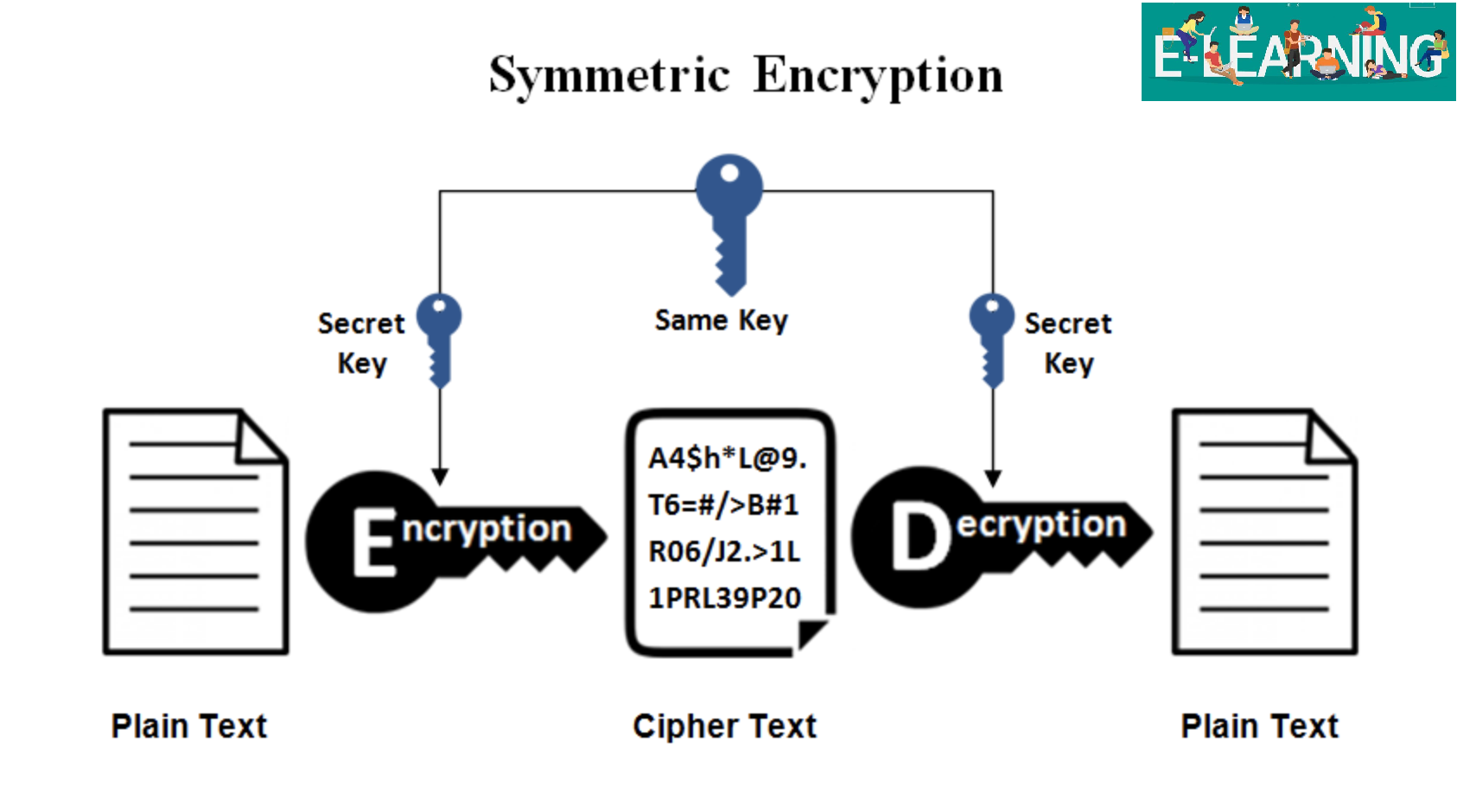
In this software implementation, the first step can generate odd numbers directly.

If it passes, output the presumed prime numbers.

Perform advanced prime test ( Miller-Rabin algorithm).

If it passes, continue to the third step.

Do a primality test with small prime numbers ( Sieve of Eratosthenes).

Pre-select random numbers of given bit length.

Nowadays, practical systems require the key length to be no less than 2048 bits, with corresponding \(p\) and \(q\) about 1024 bits each.Ī general effectiveness method for generating such large random prime numbers is a probability-based randomization algorithm, which proceeds as follows: \(N\) is the length of the RSA key, the larger the more secure. The first step in constructing the RSA encryption system is to generate two large prime numbers \(p\) and \(q\), and calculate the modulus \(N=pq\). The security of the RSA encryption algorithm is built on the mathematical challenge of factoring the product of two large prime numbers.

Donald Knuth（American computer scientist, mathematician, and professor emeritus at Stanford University, the 1974 recipient of the ACM Turing Award, often called the "father of the analysis of algorithms"） Generating Large Primes Random numbers should not be generated with a method chosen at random.